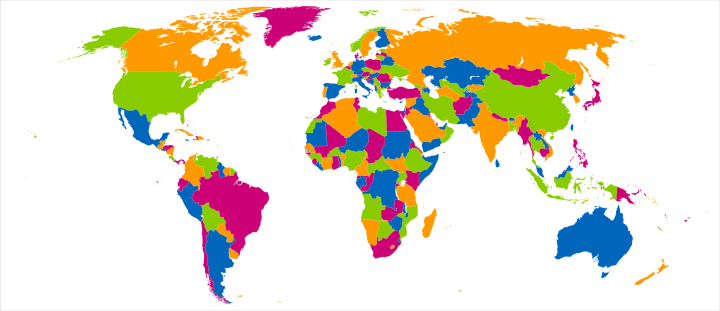
The map shows the four colour theorem in practice.
The theorm states that:
… given any separation of a plane into contiguous regions, producing a figure called a map, no more than four colors are required to color the regions of the map so that no two adjacent regions have the same color. Adjacent means that two regions share a common boundary curve segment, not merely a corner where three or more regions meet.
In actual, fact the map uses 5 colours, if you include the white used for the oceans, although it would still technically be possible to draw a world map using only 4 colours, if landlocked countries shared the same colour as the ocean.
Want to read more on the subject? The good news is that there’s a surprising number of books about it:
- Four Colors Suffice: How the Map Problem Was Solved
- The Four-Color Theorem: History, Topological Foundations, and Idea of Proof
- The Four Colour Theorem
- Graphs, Colourings and the Four-Colour Theorem
Enjoy this map? Please help by sharing it:


Will Bishop says
The four-color theorem does not prove that the world map can be four-colored, because some countries consist of non-contiguous regions (like the U.S., Russia, and Azerbaijan). It happens to work out anyway due to the placement of those countries.
PabloExpox says
Certainly. It was and with me. We can communicate on this theme.
Jo says
Disgusting map. It even shows Taiwan is part of China. I don’t know how much you have received from the Chinese gov to design such a misleading and disgusting map.
Max says
Good stuff, it doesn’t show written company’s all over it